RiVAE
Riemannian Geometric Generation via Epistemic Graphs Instead of sampling from a fixed Gaussian prior $z \sim \mathcal{N}(0, I)$, RiVAE generates data by navigating through the learned latent geometry. A well-trained VAE on MNIST defines a 2D latent space, but rather than treating it as flat, I reinterpret it as a Riemannian-like manifold induced by the model’s own epistemic structure — namely, its local uncertainty and global density. The MNIST dataset in latent space: In the RiVAE framework, every latent coordinate $z$ carries two key epistemic quantities: Together they define a surrogate line element: $$d\mathcal{l} = (1 + \alpha_u u(z) + \alpha_p p(z)) |z_i - z_j|_2$$ Where $U$ and $P$ penalize motion toward uncertain or low-density regions. This metric — termed UDLD (Uncertainty and Density-aware Latent Distance) — effectively bends the Euclidean latent space according to the model’s epistemic beliefs. A k-nearest neighbor (kNN) graph built from UDLD distances discretely approximates the manifold’s chart structure. Edges implicitly align with geodesics because the UDLD penalization discourages connections that cross uncertain or low-density regions — effectively tracing along the manifold’s high-confidence surface. However, unlike deterministic geodesic solvers, this graph-based construction enables non-deterministic trajectory generation. At each step, the model can probabilistically select the next node among the top-k neighbors, with transition probabilities biased by edge weights or curvature penalties. Thus, trajectories through latent space become stochastic realizations of geodesic motion — a diffusion-like walk across epistemic geometry, not merely interpolation. Because full pairwise UDLD computation scales as $O(N^2)$, direct distance matrices are infeasible for large datasets. Instead, RiVAE employs a sampled-batch approximation, computing local UDLD neighborhoods within limited subsets while always including the start and target points. This is not merely a computational trick — it echoes how continuous geodesics are integrated locally: dense local information near the current region of interest suffices to maintain global consistency of the path. Once the kNN graph is constructed, generation proceeds as a geodesic walk between latent points. Each intermediate latent code is decoded into an image, yielding a smooth semantic trajectory across the manifold. The resulting animation reveals a discrete geodesic on the epistemic manifold — each frame a valid MNIST digit, transitioning smoothly in semantic space without leaving the data support. Such non-deterministic paths can represent families of valid interpolations, sampling multiple epistemically consistent routes between two data modes. RiVAE transforms a conventional VAE into a geometric generator, embedding epistemic awareness directly into the latent topology. Beyond smooth generation, this opens possibilities for: Future work may generalize this to higher-dimensional latent spaces by learning Riemannian metrics directly via pullback Jacobians or graph Laplacians — bridging epistemic geometry and intrinsic generative control.

Repository (private)
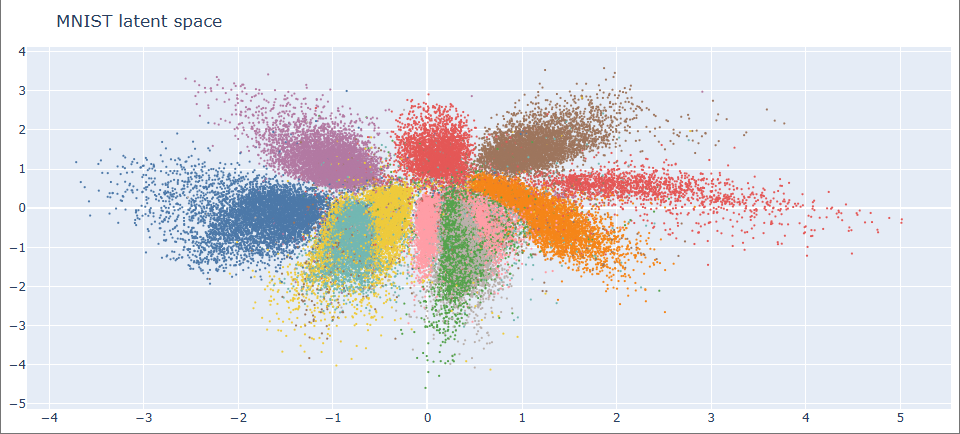

Epistemic Geometry in Latent Space
From Metric to Graph
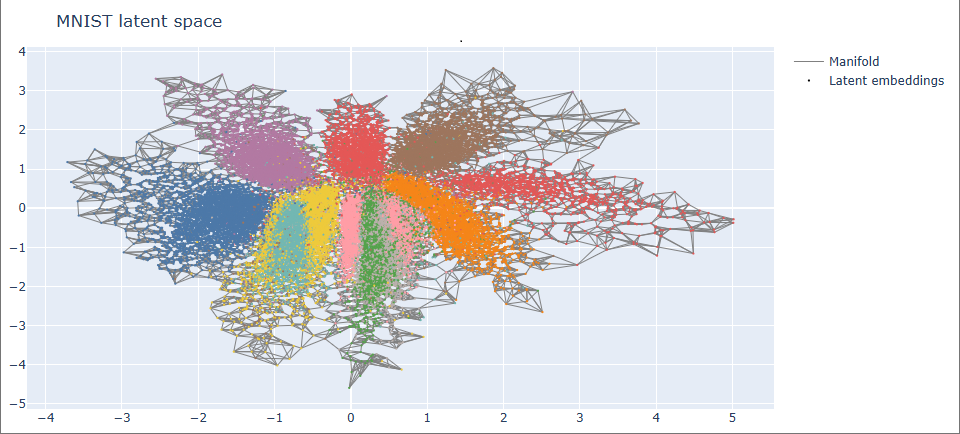

Local Approximation over Global Computation
Geometric Generation
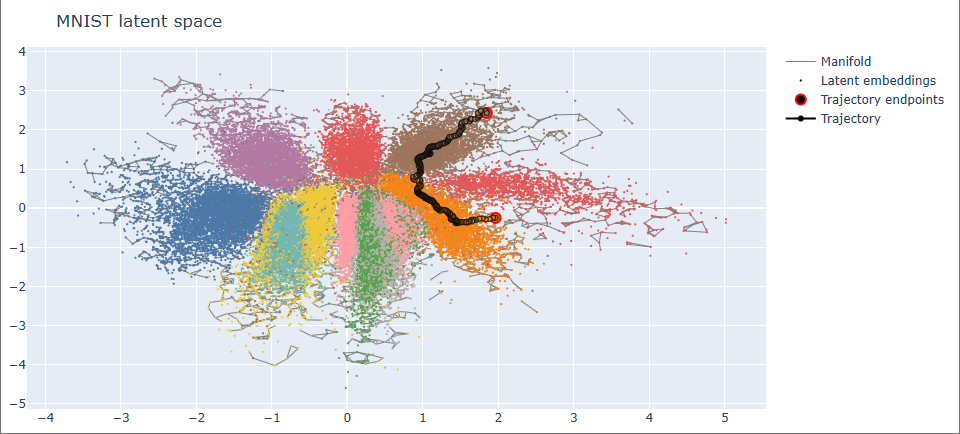

Start End Transition 



Outlook